Joanna Nikodem
PŁASZCZAKI I GRA W ŻYCIE

Czy Internet przyczynił się do zmiany pojęć „prowincja” oraz „centrum” i przedefiniowania ich według nowego kontekstu, czy wręcz odwrotnie – definicje owych pojęć istnieją od dawna w różnym kształcie, a Internet sprawił jedynie, że pewne kwestie zarysowane dekady temu nabierają fizycznego kształtu w momencie udostępnienia nowych narzędzi komunikacji w społeczeństwie? Czy schemat zachodzących zjawisk można odnaleźć w dużo wcześniejszych niż data przesłania pierwszej wiadomości z Uniwersytetu Kalifornijskiego w Los Angeles do Uniwersytetu Stanforda¹ dyskusjach na gruncie naukowym, filozoficznym, a nawet ocierających się o naturę teologiczną?

Tezą stawianą w niniejszej pracy jest stwierdzenie, że choć „rewolucja internetowa” jako szereg zmian społeczno‑kulturowych niewątpliwie ma miejsce, to charakter zachodzących zmian w większości już dawno był opisywany w dziedzinie nauk podstawowych. Patrząc zaś z perspektywy designu i sztuki, świadomość konsekwencji decyzji podejmowanych przy projektowaniu sieci wirtualnych kontaktów może mieć znaczenie strategiczne w planowanej aktywności.

Niniejszy artykuł stawia szereg otwartych pytań dotyczących rozumienia zjawisk zachodzących w społeczeństwie poprzez abstrakcyjne ujęcie pojęć odległości, wymiaru, sąsiedztwa i opartego na nim warunku przetrwania. Koncepcji wyjścia poza świat trzeciego wymiaru przy pomocy narzędzia niwelującego dotychczasowe granice przestrzenne, rozpatrywanej w postaci szansy dla ludzkości, przeciwstawiany jest matematyczny model struktury wielowymiarowej i niebezpodstawnie stawiane ostrzeżenie związane z samotnością i „wołaniem, którego nikt nie usłyszy”².

PŁASZCZAKI

Kiedy będąc w szkole podstawowej, napotykamy na zajęciach z matematyki dział geometria, naturalnie pojawiają się w naszej wyobraźni – i na kartkach zeszytu – trójkąty, czworokąty, wielokąty foremne i nieforemne, dalej okręgi, czasem elipsa. Poznajemy ich właściwości, mierzymy, wycinamy. Ich płaskość jest całkowicie naturalna, związana przecież z płaskością kartki, na której powstają. Świat opisany przez planimetrię jest płaski. Przechodząc nieco dalej, obserwujemy, jak z wielokątów powstają ściany, ściany ograniczają bryły i świat, który opisujemy równaniami, staje się przestrzenny. I w dalszym ciągu jest to doświadczenie całkiem naturalne, gdyż świat przestrzenny jest światem, w którym funkcjonujemy, w którym nasze kroki, oś widzenia, kierunek sięgania ręką wyznaczone są w trzech wymiarach. Co jednak, gdybyśmy byli gotowi na zadanie pytania o… czwartą oś?

W dziedzinie fizyki relatywistycznej rolę czwartej osi przypisuje się czasowi. Istnieje jednak inna metoda określenia czwartego wymiaru jako tak zwanego czwartego wymiaru przestrzennego. Metodę tę prezentuje między innymi Edwin Abbott w swojej fantastycznonaukowej powieści Flatlandia³, w której prowadzi czytelnika poprzez wyimaginowane krainy jednego, dwóch, trzech – a finalnie snuje wyobrażenia o owianej tajemnicą, a nawet w pewnym sensie zakazanej boskiej krainie czwartego wymiaru.

Według Abbotta Płaszczaki zamieszkują krainę dwóch wymiarów. Z zasady są wielokątami, aczkolwiek jako że świat opisany we Flatlandii jest jednocześnie satyrą odzwierciedlającą w karykaturalnej formie ówczesny, dziewiętnastowieczny układ społeczeństwa wiktoriańskiego, autor przypisuje w nim kobiecie postać odcinka, natomiast najwyższemu kapłanowi krainy idealne koło. Abstrahując od tego, jak kontrowersyjne byłoby w dzisiejszych czasach takie ujęcie ról społecznych i znaczenia płci, przyjrzyjmy się bliżej mieszkańcom Flatlandii. Żaden z mieszkańców krainy nie jest w stanie „przepełznąć” ponad swoim pobratymcem, nie jest on również w stanie zobaczyć swojego prawdziwego kształtu (ma jedynie świadomość ilości kątów i swojej foremności – lub jej braku), a otoczony krzywą zamkniętą nie jest w stanie się z niej wydostać. Dlaczego? Ponieważ żeby to uczynić, musiałby się unieść ponad płaszczyznę, do wyższego wymiaru. Dla Płaszczaka byłoby to tak samo niewyobrażalne, jak dla mieszkańca trzeciego wymiaru wydostanie się z zamkniętego pomieszczenia bez uszkadzania jego ścian.

Mieszkańcy Flatlandii żyją wyłącznie na płaszczyźnie. Ich ogląd rzeczywistości sprowadza się do widoku, jaki my, mieszkańcy trzech wymiarów, mielibyśmy, patrząc z poziomu blatu na stół bez podnoszenia wzroku. Naturalne jest zatem, że nie rozpoznają oni struktur geometrycznych inaczej niż przez ewentualne obejście kształtu dookoła, poznanie jego boków i kątów między nimi. Obiekt, który złamie granicę wymiaru i zdoła unieść się ponad płaszczyznę, znika z pola widzenia⁴.

Rysunek 1: Obiekt dwuwymiarowy dotykający swoją krawędzią linii jest widoczny dla mieszkańca przestrzeni jednowymiarowej jedynie jako odcinek. W momencie, kiedy odsunie się od linii, stanie się dla niego niewidoczny. (Rysunek oryginalny z powieści Abbotta)

Teoretycznie konstrukcja czwartego wymiaru jest jednak możliwa, mimo że nigdy nie uda nam się zobaczyć jej efektów. Weźmy jeden punkt. Z matematycznego punktu widzenia nie ma on żadnego wymiaru – długości, szerokości ani wysokości⁵. Jeśli jednak przesuniemy punkt w dowolnym kierunku i ślad tego przesunięcia zaznaczymy linią, otrzymamy odcinek, który ma już wymiar – długość. Spróbujmy teraz przesunąć odcinek w kierunku, który nie jest kierunkiem przesunięcia punktu, i również zaznaczmy cały ślad przesunięcia. Otrzymaliśmy figurę, która ma już dwa wymiary, jest ograniczona czterema odcinkami, a cztery punkty stanowią jej wierzchołki. Kontynuując ten proces, przesuńmy otrzymany czworokąt w kierunku, który nie był ani kierunkiem przesunięcia punktu, ani całego odcinka. Po zaznaczeniu śladu otrzymamy prostopadłościan – ograniczony sześcioma wielokątami, o ośmiu wierzchołkach. Czy moglibyśmy teraz przesunąć prostopadłościan, otrzymując bryłę wychodzącą w czwarty wymiar? Biorąc pod uwagę proces konstrukcji bryły, oczywiście tak. Co więcej, wiadome jest, że tak powstała bryła byłaby ograniczona ośmioma prostopadłościanami (kolejne liczby struktur ograniczających to 0, 2, 4, 6, 8), posiadała 16 wierzchołków (1, 2, 4, 8, 16), jest możliwe narysowanie jej siatki i posiada nazwę – tesserakt.

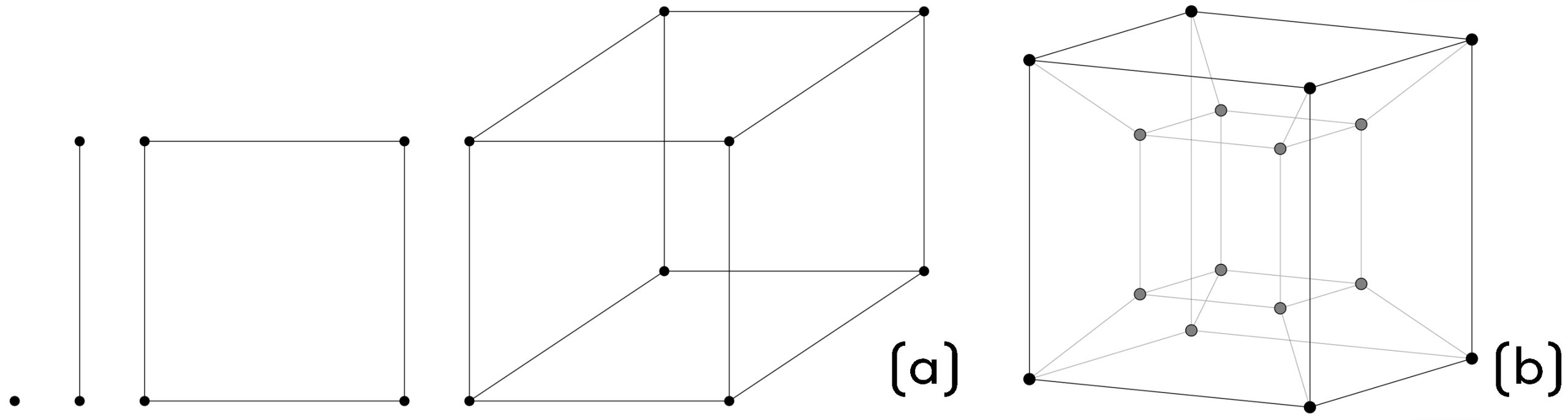
Rysunek 2: (a) konstrukcja przestrzeni trójwymiarowej przez przesunięcie kolejno punktu, odcinka i prostokąta, (b) tesserakt – wyobrażenie połączeń krawędzi w bryle czterowymiarowej

Rysunek 2: (a) konstrukcja przestrzeni trójwymiarowej przez przesunięcie kolejno punktu, odcinka i prostokąta, (b) tesserakt – wyobrażenie połączeń krawędzi w bryle czterowymiarowej

Poprzez analogię (wnioskowanie o pewnych właściwościach omawianego przedmiotu na podstawie jego podobieństw do innych przedmiotów) skonstruowaliśmy czwarty wymiar. Teoretycznie. Potrafimy konstruować bryły w czwartym wymiarze, określać ich wzajemne położenie i proporcje. Jedyne, czego nie jesteśmy, jako istoty przestrzeni trójwymiarowej, w stanie osiągnąć, to ujrzenie, a nawet wyobrażenie sobie takiej bryły.

Ćwiczenie, jakiemu została poddana wyobraźnia Czytelnika w powyższym akapicie, miało na celu pozbycie się granic rutynowego myślenia i otworzenie nowej przestrzeni dla skojarzeń i interpretacji związanych z przenikaniem się światów – rzeczywistego i wirtualnego, w szczególności zaś sąsiedztwu i komunikacji w obu światach.

Koncepcja określenia Internetu jako czwartego wymiaru społecznego pojawia się w literaturze między innymi w książce Laurence’a Scotta The Four‑Dimensional Human⁶. Rozróżnia on w swoim tekście dwie odrębne przestrzenie: cyberspace (przestrzeń wirtualna) i meatspace⁷ (przestrzeń kontaktów w świecie rzeczywistym). Przestrzenie te pozostawały równoległe do momentu, kiedy łączącym je portalem przestał być modem, a nowe standardy połączenia pozwoliły na nieprzerwane przenikanie się obu światów. Czym zatem skutkowało owo połączenie? Scott wskazuje szereg zachowań i stanów w życiu społecznym, jakich nie obserwowano (a przynajmniej nie z taką intensywnością) do momentu, kiedy każdy z obywateli został zaopatrzony w technologię, która pozwala oderwać się od fizyczności trzech wymiarów i zniknąć z pola widzenia (czy też interakcji) z otoczeniem, a jednocześnie pojawić się (mentalnie) w zupełnie innych okolicznościach. Faktem jest, że samo takie oderwanie nie jest nowym dla człowieka stanem, jeśli wspomnimy o fizycznych i psychicznych symptomach apatii, tęsknoty czy zakochania – nowym zjawiskiem jest jednak to, że tym razem osoba znikająca z przestrzeni fizycznej prowadzi całkiem świadome i nierzadko intensywne życie w innej rzeczywistości. Widząc zatem osobę siedzącą razem z nami w pomieszczeniu, niekoniecznie musimy mieć możliwość wejścia z nią w interakcję, może ona zniknąć z naszego obszaru kontaktu, analogicznie jak opisuje to Abbott w odniesieniu do obywatela Flatlandii, który unosząc się ponad płaszczyznę, znika jednocześnie z pola widzenia pozostałych istot dwuwymiarowych.

Wydostając się poza ograniczenia przestrzenne zyskujemy zdolność przekraczania granic, co daje nam możliwości poszerzania kontaktów analogicznie, jak w przypadku Płaszczaków odgrodzonych linią, kiedy przynajmniej jeden z nich nabędzie zdolność uniesienia się ponad przeszkodą. Powieść Abbotta niesie jednak również pewne ostrzeżenie. Istota, raz przekroczywszy swoje ograniczenia związane z wymiarem, przestaje należeć do swojego dawnego życia na zawsze. Kwadrat, poznawszy za sprawą Kuli będącej jego przewodnikiem, przestrzeń trzeciego wymiaru, powróciwszy do swojego świata, nie tylko doznaje ciągłego niepokoju i pragnienia powrotu do wymiaru nadrzędnego, lecz jednocześnie musi ukrywać swoje doświadczenie zagrożony niezrozumieniem wśród współmieszkańców, co potęguje jego poczucie samotności.

Do kwestii samotności w wielu wymiarach powrócimy w dalszej części tekstu.

CENTRUM I PERYFERIE

Spojrzenie na sieć powiązań internetowych jako na czwarty wymiar pozwala usystematyzować wyraźną zmianę w odczuwaniu bliskości, sąsiedztwa, kontaktu, jaka zaszła w ciągu ostatniego ćwierćwiecza. Nie mówimy tu jednak o fizycznym ani duchowym odczuwaniu kontaktu. Zjawisko to należałoby w przypadku internetu rozumieć czysto praktycznie. Mamy bliski kontakt z kimś, kogo fizycznie być może nigdy nie widzieliśmy w rzeczywistości. Możemy stanowić wraz z innymi osobami centrum‑wnętrze jakiejś struktury, nawet jeśli w fizycznym rozumieniu drogi łączące nasze miejsca pobytu raczej oplatałyby powierzchnię Ziemi, niż dążyły do połączenia w jednym punkcie. Pojęcie odległości zatraciło całkowicie swoje pierwotne znaczenie dzięki konstrukcji struktury wynoszącej dotychczasowy sposób komunikowania się ludzi w kolejny wymiar.

W matematyce odejście od euklidesowej koncepcji wyznaczania odległości między dwoma punktami w oparciu o ich współrzędne w układzie kartezjańskim nie jest jednak nowością. Zarówno pojęcie odległości, jak i związany z nim kształt kuli (koła), który na potrzeby niniejszych rozważań może być analogią do centrum i jego otoczenia (peryferii), mają swoje alternatywne definicje, bezpośrednio związane z praktycznym aspektem ich zastosowania. Z punktu widzenia kompletności teorii matematycznej rygorystycznie trzymają się one jednak wyznaczonych warunków stawianych konstrukcji pojęcia odległości.

Tak więc w przypadku poruszania się w warunkach miejskich znalezienie najbliższej drogi z punktu A do punktu B sprowadzałoby się do znalezienia najkrótszego przejścia ulicami miasta; nie jest możliwe przejście na ukos przez budynki. Jeśli układ ulic w mieście byłby prostopadły, mówilibyśmy o tak zwanej odległości taksówkowej.

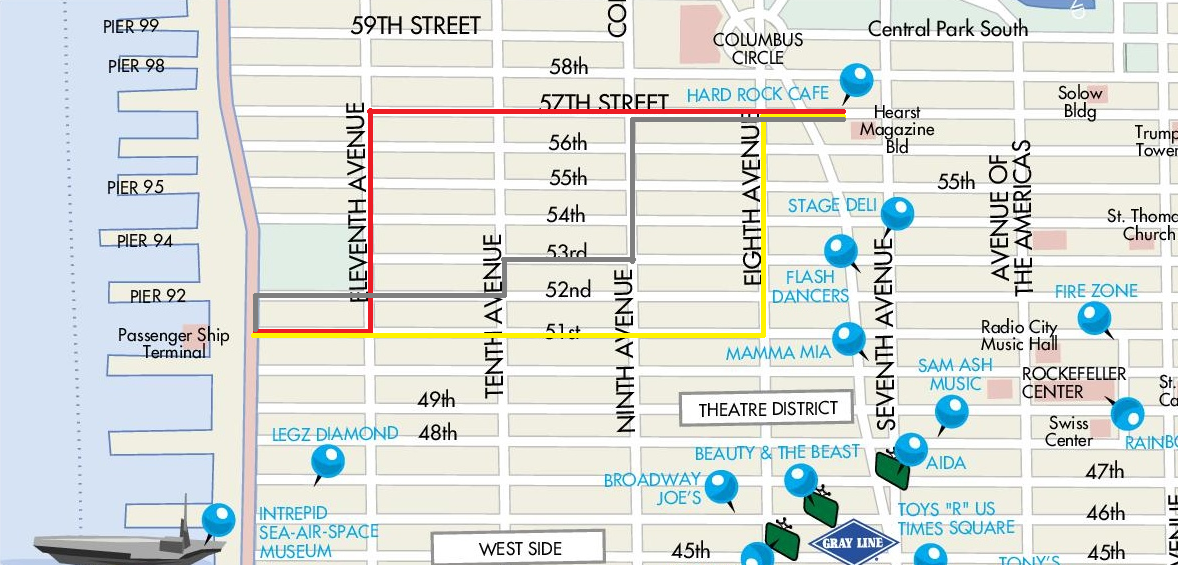
Rysunek 3: Określenie odległości jako sumy odcinków równoległych i odcinków do nich prostopadłych (w trzech wariantach) na podstawie przejścia z Hard Rock Cafe do terminalu promowego przy West Side na Manhattanie

 (ilustracja na podstawie treści udostępnianej przez Ontheworldmap ⁸)

Odległość ta, zdefiniowana jako suma odcinków, jakie należałoby przejść ulicami równoległymi, wraz z sumą odległości, jaką przeszlibyśmy ich przecznicami, spełnia warunki odległości, jakie określone są w trzech puntach⁹:

•  odległość między punktami wynosi 0 wyłącznie wtedy, gdy punkty są tożsame;
•  odległość z punktu A do punktu B wynosi dokładnie tyle samo co z punktu B do punktu A (warunek symetrii);
•  odległość bezpośrednia między punktami A i B nie może być większa niż długość drogi z punktu A do punktu B przechodzącej przez dodatkowy punkt C (warunek trójkąta).

Poruszanie się komunikacją miejską, a zwłaszcza podmiejską lub krajową (jak linie kolejowe czy autobusowe) narzucałoby kolejne ograniczenia co do wyznaczenia przejść między punktami, wynikające z tego, że często bezpośredniego połączenia między miejscami po prostu nie ma i jedyne, co możemy zrobić, to skorzystać z punktu przesiadkowego lub magistrali. Dobrym przykładem jest poruszanie się między niektórymi miejscowościami w pasie nadmorskim – chcąc odwiedzić sąsiednią miejscowość lokalnymi środkami transportu, bardzo często musimy albo cofnąć się w głąb lądu do większego miasta i tam przesiąść się na inny autobus (punkt centralny), albo dotrzeć do wybrzeża i skorzystać z przewozu statkiem turystycznym (magistrala). Obie koncepcje są również poprawne pod względem matematycznej definicji odległości i noszą nazwy odpowiednio metryki kolejowej i metryki typu rzeka.

We wszystkich wymienionych metrykach da się wyznaczyć kulę jako zbiór wszystkich punktów oddalonych od zadanego środka o nie więcej niż wskazaną odległość. Nie w każdym przypadku tak wyznaczony zbiór odpowiada potocznemu rozumieniu pojęcia kuli, jest jednak w pełni uzasadniony zarówno formalnie, jak i praktycznie i analizując kształt powstałej bryły, możemy z łatwością odnieść go do socjoekonomicznych pojęćcentrum, obrzeży i peryferii. Czy dałoby się przenieść którąkolwiek z klasycznych definicji odległości na potrzeby Internetu?

CENTRUM INTERNETU

Jednym z przełomowych rozwiązań technologicznych służących do określenia istotności danej strony WWW, a co za tym idzie wskazania wyszukiwarce priorytetu w prezentowaniu wyników zapytania, był wskaźnik PageRank¹⁰. Podstawą jego działania była ilość i jakość odnośników prowadzących z innych stron do danej strony, co w jednym zdaniu podsumować można stwierdzeniem, że „strona WWW jest ważna, jeśli prowadzą do niej odnośniki z wielu ważnych stron”¹¹.

Wskaźnik PageRank strony B (mnożony przez tzw. współczynnik tłumienia równy zazwyczaj 0,85) jest dodawany do wartości PageRank strony A, jeśli strona B kieruje użytkownika do strony A poprzez hiperłącze. W momencie gdy na stronie B znajduje się więcej niż jeden link, wtedy PageRank strony B dzieli się równomiernie na liczbę linków. Tym samym w sytuacji, gdy na stronie tej znajduje się 10 linków (w tym jeden do strony A), wówczas strona A otrzymuje 1/10 wartości PageRank strony B.

Jak zatem określić pojęcia odległości, centrum i peryferii, biorąc pod uwagę to, że odległość między stronami A i B (czy też profilami w portalach społecznościowych) mierzona jest nie w jednostkach długości, ale w ilości węzłów, które trzeba przejść, pokonując tę drogę? Można przyjąć, że struktura powiązań internetowych jest strukturą grafową, w której węzły stanowią konkretne adresy stron i profili, a krawędzie odzwierciedlają linki między stronami lub fakt obserwowania profilu (w obu przypadkach jest to zależność niesymetryczna – zatem mówimy o grafie skierowanym). W teorii grafów jako definicję ścieżki przyjmuje się ciąg krawędzi wraz z kolejnymi wierzchołkami występującymi na ścieżce. Odległością z węzła A do węzła B nazywa się zatem długość ścieżki z A do B, jeśli taka istnieje – w przeciwnym przypadku określa się odległość jako nieskończoną¹². Definicja odległości oparta na długości ścieżki spełnia wszystkie warunki bycia metryką (jakie wymieniono w poprzedniej części rozdziału), w pełni uzasadnione jest zatem przeniesienie pojęć opartych na metryce, w tym pojęcia kuli o zadanym środku i promieniu, na przestrzeń metryczną grafową. Kulą o promieniu r i środku K będzie zbiór węzłów odległych od K o nie więcej niż r, więc nie więcej niż r‑1 węzłów pośrednich będzie stało na ścieżce od środka kuli, do należącego do niej punktu A.

Mając do dyspozycji pojęcie kuli, możemy oprzeć na nim pojęcie centrum i peryferii. Jeśli przyjmiemy, że centrum stanowi właśnie kula, to będą do niego należeć wszystkie strony, do których można dotrzeć, zaczynając ze stanowiącego jej środek adresu w nie więcej niż r krokach. Pozostałe adresy są względem tej strony peryferiami.

Czy jednak o to dokładnie chodziło? Czy tak wyznaczone centrum jest w jakikolwiek sposób centrum Internetu? Raczej nie. Definicja kuli stanowi o centrum lokalnym, związanym z konkretnym punktem startowym – nijak ma się jednak do rozumienia centrum jako miejsca najważniejszego – nośnika zmian, aktywności, czy punktu odniesienia w ujęciu globalnym. Nie da się wykreować centrum, umieszczając na stronie ponadprzeciętną liczbę odnośników. A raczej dało się, w początkowej fazie masowego dostępu do Internetu. Wspomniany wyżej wskaźnik PageRank miał na celu weryfikację tak generowanych centrów poprzez analizę ilości i jakości linków prowadzących nie ze strony, ale do niej. I to jednak okazało się niewystarczające. Być może w ujęciu ekonomicznym, jako wskaźnik opłacalności kampanii reklamowych, wyznaczanie stron o najwyższych wskaźnikach globalnych odgrywało swoją rolę – w ujęciu społecznym okazało się jednak nie spełniać rosnących wymagań, a obecne algorytmy wyszukiwania znacznie bardziej opierają się na personalizacji wyniku. Walka o bycie „w centrum” nabiera zatem zupełnie nowego wymiaru.

GRA W ŻYCIE

Porzucając na chwilę kwestię wymiaru i odległości, skupmy się wyłącznie na pojęciu sąsiedztwa i jego wpływie na rozwój jednostki – samą jednostkę interpretując zaś na przykład jako zalążek, centrum pracy i twórczości pojedynczego artysty, projektanta lub autora publikującego i budującego swoją aktywność w mediach społecznościowych.

Cykl istnienia strony internetowej czy profilu w portalu społecznościowym jest oparty na ciągłym balansie między życiem a śmiercią. W niniejszym wątku przywołany zostanie aspekt przeludnienia i osamotnienia jako wskaźników zwiastujących fazę zmierzchu – bądź początek rozwoju badanego adresu. Dyskusja prowadzona w poprzednim rozdziale, związana z kwestią centrum i peryferii w Internecie, pozwoliła zdefiniować pojęcie sąsiedztwa jako zbioru wszystkich profili odległych o jeden krok od zadanego środka – czyli połączonych bezpośrednio z badanym profilem poprzez obserwowanie, nawiązanie znajomości czy dołączenie do grupy. Czy można zatem przyjąć, że w celu podniesienia wartości własnego miejsca w Internecie trzeba dążyć za wszelką cenę do poszerzania sąsiedztwa przez gromadzenie jak największej ilości kontaktów?

W odpowiedzi na to pytanie posłużymy się przykładem jednego z pierwszych symulatorów rozwoju populacji opartego wyłącznie na definicji sąsiedztwa i kilku prostych regułach. Gra w życie (The game of life) jest jednym z bardziej znanych przykładów automatu komórkowego, nie tylko ze względu na swój potencjał naukowy, ale również wkład w dziedzinę kultury i sztuki. Wymyślony w 1970 roku przez brytyjskiego matematyka Johna Conwaya, a spopularyzowany przez Martina Gardnera na łamach „Scientific American”¹³, posłużył zarówno do celów badawczych, dając możliwość obserwowania procesów rozwoju, zanikania bądź stabilizacji struktur, jak i rozrywkowych w postaci gier i łamigłówek logicznych.

Gra toczy się na planszy (skończonej lub nieskończonej), podzielonej na kwadratowe komórki. Każda komórka ma ośmiu sąsiadów – komórki tworzące sąsiedztwo przylegają do niej bokami lub narożnikami, tworząc tzw. sąsiedztwo Moore’a. Każda komórka może znajdować się w jednym z dwóch stanów: może być albo „żywa” (aktywna), albo „martwa” (nieaktywna). Przeżycie danej komórki w bieżącym cyklu definiowane jest w następujący sposób:

•  martwa komórka, która ma dokładnie trzech żywych sąsiadów, staje się żywa w następnej jednostce czasu;
•  żywa komórka, która ma dwóch albo trzech żywych sąsiadów, pozostaje nadal żywa;
•  przy każdej innej liczbie sąsiadów żywa komórka umiera – z „samotności” przy mniej niż dwóch żywych sąsiadach bądź z „przeludnienia”, gdy sąsiadów jest czterech lub więcej.

Rysunek 4: Przykładowy stan automatu komórkowego w Grze w życie Conwaya

Jak reguły gry Conwaya mają się do cyklu życia w Internecie? Niezależnie od tego, czy profil bądź strona internetowa zakładane są spontanicznie, czy też ich powstanie poprzedza cykl analiz rynkowych i przygotowań, kluczową kwestią jest zebranie wokół tworzonego miejsca określonej społeczności. Skupimy się w tym miejscu na bardzo konkretnym wątku będącym próbą opisu ewolucji rozmiaru i charakteru tejże społeczności. Przyjmijmy, podobnie jak u Conwaya, że jedna komórka to jeden osobnik – w naszym przypadku profil internetowy. Załóżmy ponadto, że do jego sąsiedztwa zaliczany jest każdy inny profil, z którym ten jest w aktywnym kontakcie, co może w tym przypadku oznaczać wzajemne komentowanie treści, nawiązywanie dialogu czy oznaczanie się w postach. Musimy tu oczywiście odstąpić od geometrii płaskiej uwzględnionej w oryginalnej Grze w życie z tej przyczyny, że na płaszczyźnie z ośmiosąsiedztwem Moore’a nie dałoby się przypisać komórkom takiej liczby kontaktów, jaka dotyczy profili internetowych – z matematycznego punktu widzenia nie jest to jednak problemem. Komórce możemy przypisać dwa stany. Analogią do komórki martwej (nieaktywnej) Conwaya byłby profil użytkownika uśpiony, bierny, o ograniczonej aktywności w sieci, bądź nastawiony wyłącznie na odbiór wiadomości, nie zaś na jej przekaz. Odpowiednikiem komórki żywej byłby natomiast profil posiadający dużą ilość aktywnych kontaktów, z którymi regularnie wymienia się treścią, jest nastawiony na rozwój i poszerzanie zakresu działania, co może również uwzględniać kontrakty reklamowe i działania influencerskie.

Z pozoru wydawać by się mogło, że zdobywanie kolejnych kontaktów za każdym razem jest bezwzględnie pożądane i gwarantuje sukces profilu. Jednak przyłożenie do powyższego opisu zasad działania automatu komórkowego¹⁴ prowadzi do zupełnie przeciwnych wniosków. W każdym przypadku istnieje określona wartość krytyczna liczby kontaktów, poza którą dodanie kolejnego nowego pociąga za sobą utratę dotychczasowych, co więcej, proces ten może przebiegać lawinowo, prowadząc do utraty wartości (czy śmierci?) całego profilu. Zjawisko utraty kontaktów poprzez przekroczenie granicznej liczby kontaktów zostało zbadane na podstawie portali Instagram¹⁵ i Twitter¹⁶ i jest ściśle związane z zachowaniem użytkowników ujętym w schemat follow/unfollow, polegającym na intensywnym rozsyłaniu zaproszeń do śledzenia własnego profilu przy jednoczesnym dodaniu do obserwowanych profili zapraszanych. W razie nieuzyskania zainteresowania ze strony zapraszanych gości zarządzający profilem usuwa również swoje obserwowania dla danego profilu. Proces ten, zwłaszcza przeprowadzany na szeroką skalę i wspomagany przez działanie botów, nie wnosi ostatecznie wartości dodanej, ponieważ jest działaniem sztucznym, kontakt z zapraszanymi osobami jest nierzadko jednorazowy i – z braku dalszej interakcji – ostatecznie ucinany przez któregoś z użytkowników. Co więcej, jako wprowadzający chaos w rankingach popularności profili jest przez wiele portali zakazany, o czym informują zapisy regulaminów¹⁷.

KLĄTWA WIELOWYMIAROWOŚCI

Wracając do poruszanych we wcześniejszych rozdziałach kwestii wymiaru i odległości, przyjrzyjmy się teraz „gęstości” kontaktów w mediach społecznościowych. Postawmy pytanie: czy dodanie nowego kontaktu do grupy znajomych poszerzy, czy też, paradoksalnie, może zawęzić możliwość skutecznej komunikacji w gronie istotnych dla nas użytkowników?

Rozumując od strony geometrii, jeśli rozmieścimy pewną ilość punktów w jednostce przestrzennej, na przykład pięć punktów na jeden centymetr kwadratowy, a następnie pozwolimy danym punktom „rozbiec się” w przestrzeni o jeden wymiar większej – w tym przypadku będzie to sześcian o boku jednego centymetra – gęstość rozmieszczenia punktów raptownie spadnie. Można to sobie wyobrazić, dzieląc pierwotną przestrzeń, kwadrat o boku jednego centymetra, na mniejsze kwadraty o boku jednego milimetra, otrzymując 10 × 10 = 100 takich kwadratów. Jeśli rozmieścimy punkty tak, aby w jednej kratce znajdował się najwyżej jeden punkt, prawdopodobieństwo wylosowania kwadratu zawierającego punkt wyniesie pięć na sto, czyli 5%. Jeżeli rozszerzymy rozumowanie z kwadratu na sześcian, w wyniku podziału otrzymamy 10 × 10 × 10 = 1000 mniejszych sześcianów i jeśli utrzymamy zasadę pozwalającą w jednej kostce znaleźć się tylko jednemu punktowi, szansa na wylosowanie kostki z punktem będzie wynosiła pięć na tysiąc, czyli ledwie 0,5%. Co więcej, kula o zadanym promieniu zajmuje wraz ze wzrostem wymiaru coraz mniejszą część kostki o stałej długości krawędzi, przez co prawdopodobieństwo, że dla zadanego punktu w otaczającym go sąsiedztwie znajdzie się inny z wyróżnionych punktów, również maleje. Stąd znajdujące się we wstępie do artykułu nawiązanie do słów „In high dimensional spaces, no one can hear your scream” – jeśli twój głos rozchodzi się tylko na zadaną odległość, jest prawdopodobne, że w hiperprzestrzeni nie znajdzie się nikt, kto byłby na tyle blisko, żeby go usłyszeć…

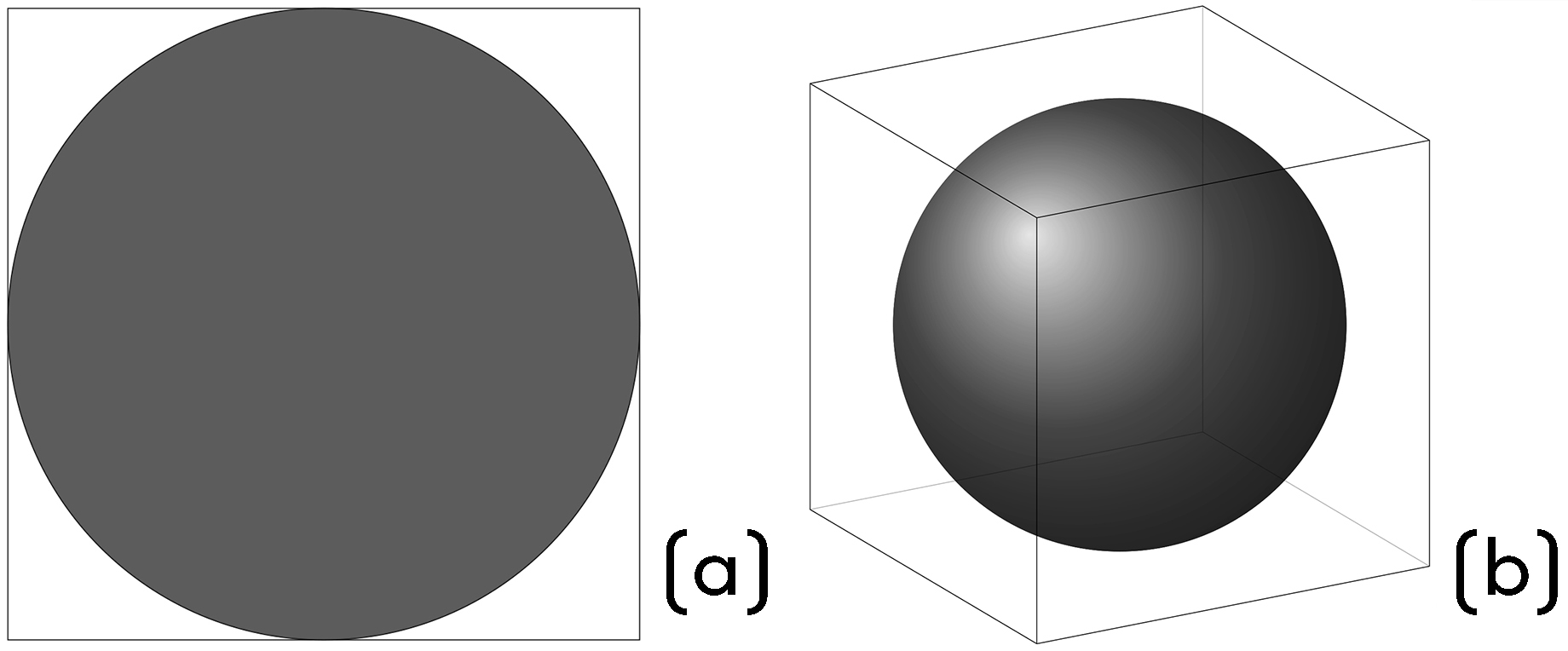
Rysunek 5: Kula w dwóch wymiarach wypełnia sobą większą część kwadratu, w który jest wpisana, niż kula w trzech wymiarach wypełnia sześcian.

Jak ma się w takim razie geometryczne rozszerzanie wymiaru do nawiązywania kolejnych kontaktów w portalach społecznościowych? Każda aktywność profilu, w tym dodanie kontaktu do grupy znajomych, polubienie, obserwowanie, dołączenie do grupy, powoduje, że algorytm dystrybuowania treści uczy się naszych preferencji i zwielokrotnia ilość proponowanych postów, dodając coraz większą ilość tych niepochodzących z naszych bezpośrednich kontaktów.

Posłużmy się konkretnie przykładem Facebooka i pytaniem: Jak Facebook dystrybuuje treści? Według oficjalnych danych¹⁸ Facebook wyświetla wiadomości na stronie głównej użytkownika, przeprowadzając analizę w czterech głównych krokach, w tym wyboru treści udostępnianych przez kontakty użytkownika, zbierania sygnałów i prognoz, z jakim prawdopodobieństwem użytkownik zareaguje na post, oraz obliczania wskaźnika trafności – jak bardzo odbiorcy będą zainteresowani danym postem.

Czy można zatem przewidzieć, kto i kiedy zobaczy treść wiadomości, którą właśnie edytujemy i wysyłamy w świat? Chcielibyśmy wierzyć, że wiadomość zostanie odczytana chociaż przez właścicieli profili, które mamy w swojej zakładce znajomych. Co jednak, jeśli dla każdego ze znajomych jesteśmy jedynie jednym z kilkuset lub nawet kilku tysięcy kontaktów, z których każdy wysyła co najmniej kilka wiadomości w tygodniu? Prawdopodobieństwo, że to akurat nasz post znajdzie się na tyle wysoko, żeby nasi znajomi ujrzeli go w na swojej stronie głównej, spada z każdym dodanym przez nich kontaktem do znajomych, podobnie, jak malała szansa na znalezienie punktu w zasięgu kuli o zadanym promieniu przy każdym zwiększeniu wymiaru, w jakim się znajduje. O ile nasz profil nie ma nad innymi przewagi w postaci trafności publikowanych treści, bliskości relacji wyrażanej częstą interakcją czy też umiejętnej konstrukcji samej wiadomości – nikt może nas nie usłyszeć. Mimo wypełnionej po brzegi zakładki „Znajomi”.