Joanna Nikodem
FLATLANDERS AND THE GAME OF LIFE

Has the Internet helped to change the concepts of ‘province’ and ‘centre’ and redefine them according to a new context, or is it the other way around: definitions of these concepts have existed for a long time in different forms and the Internet only made certain issues outlined decades ago take physical shape when new tools for communication were made available to the public? Can the pattern of the phenomena taking place be traced back much earlier than the date of the first message from the University of California in Los Angeles to Stanford University¹ in the discussions of a scientific, philosophical and even theological nature?

The thesis of the present paper is that, although the ‘Internet revolution’ as a series of socio-cultural changes is undoubtedly taking place, the nature of these changes has for the most part been described in the field of basic science for a long time. And regarding the design and art perspective, awareness of the consequences of decisions made in designing virtual networks can be strategic in the planned activity.

This article raises a number of open questions about understanding phenomena in society through abstracting the concepts of distance, dimension, neighbourhood and the survival condition based on it. The concept of transcending the world of the third dimension by means of a tool that levels existing spatial boundaries, seen as an opportunity for humanity, is contrasted with a mathematical model of multidimensional structure and an unwarranted warning related to loneliness and a ‘cry that no one will hear’.²

FLATLANDERS

In primary school, when, during the mathematics classes, we have to deal with the domain of geometry, triangles, quadrilaterals, regular and irregular polygons, also circles, sometimes ellipses naturally appear in our imagination and on the pages of our notebooks. We learn about their properties, we measure them, we cut them out. Their flatness is entirely natural, related, after all, to the flatness of the sheet of paper on which they are created. The world described by planimetry is flat. Moving on a little further, we observe how walls are formed from polygons, walls constrain solids and the world we describe with equations becomes spatial. And it is still a quite natural experience, because the spatial world is the world in which we function, in which our steps, the axis of vision, the direction of reaching with the hand are determined in three dimensions. However, what if we were prepared to ask the question about the … fourth axis?

In the field of relativistic physics, the role of the fourth axis is attributed to time. However, there is another way of defining the fourth dimension as the so-called fourth spatial dimension. This method is presented, among others, by Edwin Abbott in his science-fiction novel Flatland,³ in which he leads the reader through imaginary lands of one, two and three dimensions and, ultimately, weaves ideas of a fourth-dimensional realm shrouded in mystery and constituting, in a sense, a forbidden divine realm.

According to Abbott, the Flatlanders inhabit a realm of two dimensions. As a rule, they are polygons, although as the world described in Flatland is also a satire reflecting in caricature form the then 19th-century configuration of the Victorian society, the author assigns to the woman the form of a segment, while the highest priest of this world is assigned a perfect circle. Leaving aside how controversial such an account of social roles and the importance of gender would be today, let us take a closer look at the Flatlanders. None of the inhabitants of this land is able to ‘crawl’ over their compatriot, nor are they able to see their true shape (they are only aware of the number of angles and their formality, or lack thereof); surrounded by a closed curve, they are unable to get out of it. Why? Because in order to do so, they would have to rise above the plane, to a higher dimension. It would have been as unimaginable for the Flatlander as it would have been for an inhabitant of the third dimension to get out of a closed room without damaging its walls.

Flatlanders live exclusively on the plane. Their view of reality is reduced to the view we, three-dimensionals, would have if we were looking from table top level without lifting our eyes. It is natural, therefore, that they do not recognise geometric structures other than by possibly going around the shape, learning about its sides and the angles between them. Any object that breaks the dimensional boundary and manages to rise above the plane disappears from view.⁴

Figure 1. A two-dimensional object touching a line with its edge is visible to the occupant of a one-dimensional space only as a segment. The moment it moves away from the line, it becomes invisible to it. (Original figure from the Abbott’s novel)

In theory, however, the construction of a fourth dimension is possible, although we will never be able to see its effects. Let us take one point. Mathematically, it has no dimension: no length, width or height.⁵ However, if we move a point in any direction and mark the trace of this movement with a line, we get a segment that already has a dimension: length. Let us now try to move the segment in a direction that is not the direction of the displaced point, and also mark the entire trace of the displacement. We receive a figure that already has two dimensions, is bounded by four segments and has vertices it the form of four points. Following this process, let us move the resulting quadrilateral in a direction that was neither the direction of the displaced point nor of the whole segment. After marking the trace, we get a cuboid: bounded by six polygons, with eight vertices. Could we now move the cuboid to obtain a solid going out into the fourth dimension? Given the solid construction process, obviously yes. Furthermore, it is known that the solid created in this way would be bounded by eight cuboids (the next numbers of bounding structures are 0, 2, 4, 6, 8) and have 16 vertices (1, 2, 4, 8, 16); it is possible to draw its grid and this grid has a name: tesseract.

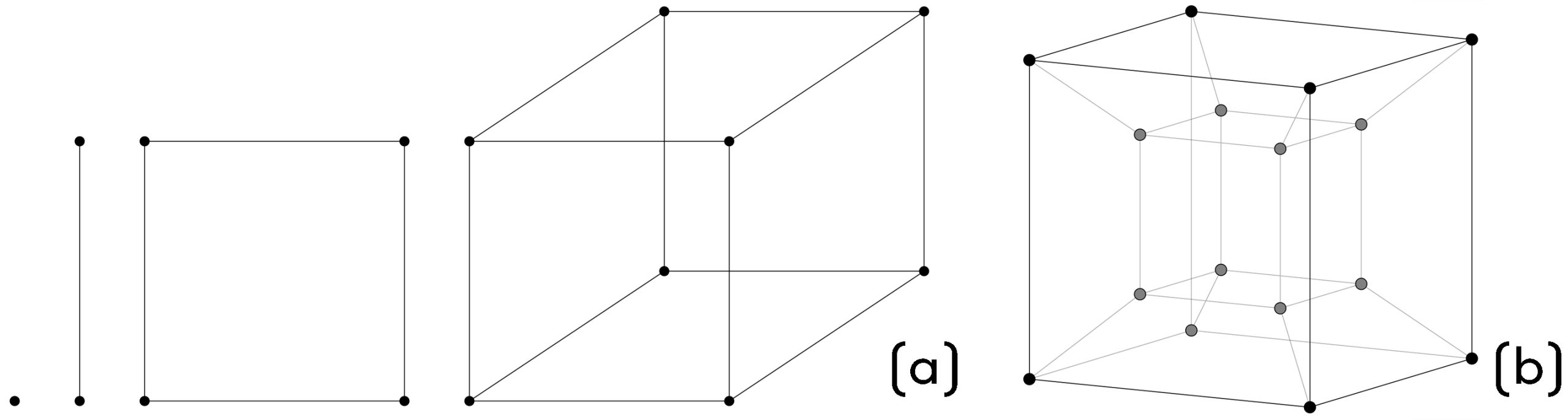
Figure 2. (a) construction of a three-dimensional space by moving a point, a segment and a rectangle sequentially, (b) tesseract: representation of the connection of edges in a four-dimensional solid

Through analogy (inferring certain properties of the object in question on the basis of its similarities to other objects), we have constructed a fourth dimension. In theory. We are able to construct solids in the fourth dimension, determine their mutual position and proportions. The only thing we, as beings of three-dimensional space, are not able to achieve is to see or even imagine such a solid.

The exercise to which the Reader’s imagination has been subjected in the above paragraph was intended to shed the boundaries of routine thinking and open up a new space for associations and interpretations related to the interpenetration of the worlds: the real and the virtual, and in particular the proximity and communication in both these worlds.

The concept of defining the Internet as a fourth social dimension appears in the literature among others in Laurence Scott’s The Four-Dimensional Human.⁶ In his text, the author distinguishes between two distinct spaces: cyberspace (virtual space) and meatspace⁷ (space of contacts in the real world). These spaces remained parallel until the portal connecting them ceased to be a modem, and new standards of connection allowed the two worlds to intermingle uninterruptedly. So, what was the result of this combination? Scott identifies a number of behaviours and states in social life that were not observed (or at least not with such intensity) until each citizen was provided with technology that allows them to detach themselves from the physicality of the three dimensions and disappear from sight (or interaction) with their surroundings, while appearing (mentally) in completely different circumstances. The fact is that such detachment itself is not a new state for humans, if we mention the physical and psychological symptoms of apathy, longing or falling in love, what is new, however, is that this time the person disappearing from physical space leads a quite conscious and often intense life in another reality. That is why seeing a person sitting in a room with us, we do not necessarily have to be able to interact with them, they may disappear from our area of contact, analogous to Abbott’s description of the Flatland citizen who floats above the plane and simultaneously disappears from the field of view of the other two-dimensional beings.

By getting beyond spatial constraints, we gain the ability to transcend boundaries, which gives us the potential to broaden our contacts analogously to Flatlanders fenced off by a line when at least one of them acquires the ability to float above the obstacle. However, Abbott’s novel also carries a warning. A being, once having transcended its dimensional limitations, ceases to belong to its former life forever. Square, having learnt, with the help of Sphere serving him as his guide, about the space of the third dimension, having returned to his own world, not only experiences constant anxiety and a desire to return to the superior dimension, but at the same time has to hide his experience at risk of being misunderstood among his fellow inhabitants, which intensifies his sense of loneliness.

We will return to the issue of loneliness in its many dimensions later in the text.

CENTRE AND PERIPHERY

Looking at the on-line network of relations as a fourth dimension makes it possible to systematise the clear change in the feeling of proximity, neighbourliness and contact that has occurred over the last quarter of a century. However, we are not talking about the physical or spiritual feeling of contact. In the case of the Internet, this phenomenon should be understood in a purely practical sense. We are in close contact with someone we may never have physically seen in real life. We may constitute, together with others, the centre-interior of some structure, even if, in the physical sense, the paths connecting our places of residence would wrap around the surface of the Earth rather than aim to connect at a single point. The notion of distance has completely lost its original meaning thanks to the construction of a structure that takes the past way people communicate into another dimension.

In mathematics, however, the departure from the Euclidean concept of determining the distance between two points based on their Cartesian coordinates is not new. Both the concept of distance and the associated sphere (circle) shape, which, for the purposes of this discussion, may be an analogy for the centre and its surroundings (periphery), have their alternative definitions, directly related to the practical aspect of their application. However, from the point of view of the completeness of mathematical theory, they rigorously adhere to the prescribed conditions placed on the construction of the concept of distance.

Thus, when navigating in an urban setting, finding the nearest route from point A to point B would come down to finding the shortest route through the city streets; it is not possible to walk diagonally through buildings. If the street layout of the city was perpendicular, we would be talking about the so-called taxi distance.

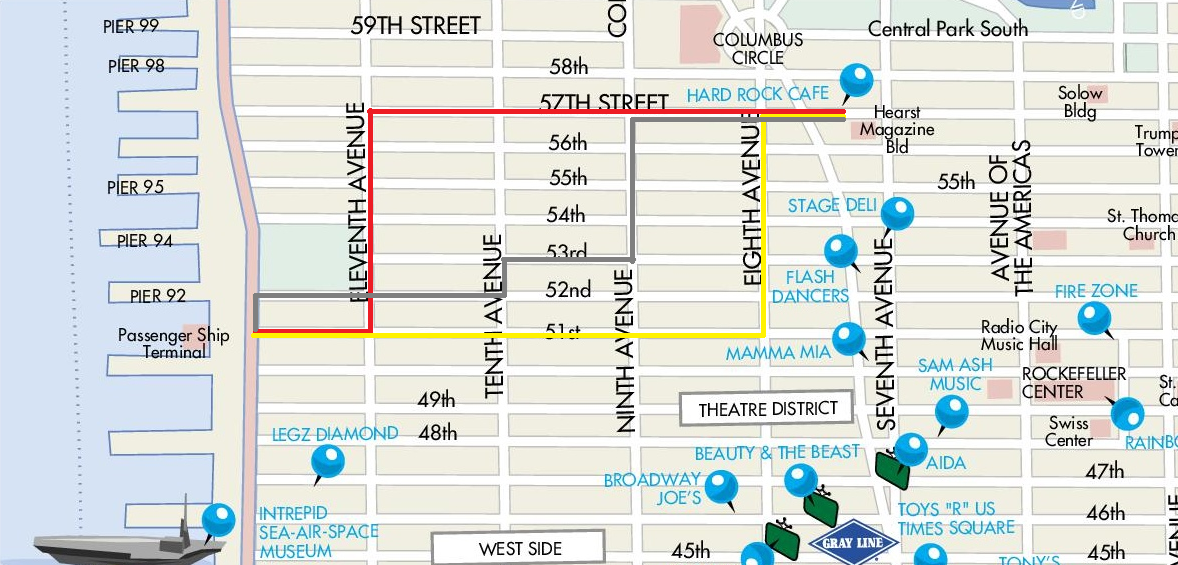
Figure 3. Determination of distance as the sum of parallel and perpendicular segments (in three variations) based on the walk from the Hard Rock Cafe to the ferry terminal on Manhattan’s West Side

(illustration based on content provided by Ontheworldmap ⁸)

This distance, defined as the sum of the distances that would have to be traversed by parallel streets, together with the sum of the distances that would have to be traversed by their respective blocks, satisfies the distance conditions defined by the three points:⁹

• the distance between points is 0 only if the points are identical;

• the distance from point A to point B is exactly the same as from point B to point A (symmetry condition);

• the direct distance between points A and B must not be greater than the length of the path from point A to point B passing through an additional point C (triangle condition).

Moving by public transport, especially suburban or national one (e.g., railway or bus lines) would impose further restrictions on the designation of point-to-point transitions, due to the fact that often there is simply no direct connection between places and all we can do is use an interchange point or a throughway. A good example is getting around between certain towns in the coastal zone – if we want to visit a neighbouring town by local transport, we very often have to either backtrack inland to a larger town and change to another bus there (central point) or reach the coast and use a tourist boat service (throughway). Both these concepts are also correct in terms of the mathematical definition of distance and are named, respectively, rail metrics and river-type metrics.

In all the metrics mentioned, it is possible to determine a sphere as the set of all points that are located no further than the indicated distance from the given centre. Not in every case does such a set correspond to the colloquial understanding of the concept of a sphere, but it is fully justified both formally and practically, and by analysing the shape of the resulting solid, we can easily relate it to the socio-economic concept of centre, margin and periphery. Would it be possible to transfer any of the classical definitions of distance to the Internet?

CENTRE OF THE INTERNET

One of the technological breakthroughs for determining the relevance of a given web page and thus indicating the search engine’s priority in presenting the results of a query was the PageRank index.¹⁰ It was based on the number and quality of links leading from other sites to a given page, which can be summed up in one sentence by the statement that ‘a website is valid if there are links to it from many other valid sites’.¹¹

The PageRank indicator of site B (multiplied by the so-called damping coefficient of usually 0.85) is added to the PageRank value of site A if site B directs the user to site A via a hyperlink. When there is more than one link on site B, then the PageRank of site B divides evenly into the number of links. Thus, if there are 10 links on this site (including one to site A), then site A receives 1/10 of the PageRank of site B.

How, then, do we define the concepts of distance, centre and periphery, given that the distance between sites A and B (or social network profiles) is measured not in units of length, but in the number of nodes it takes to travel that distance? It can be assumed that the structure of web links is a graph structure, in which the nodes are the specific addresses of sites and profiles, and the edges reflect the links between sites or the fact of observing a profile (in both cases it is an asymmetrical relationship – so we are talking about a directed graph). In graph theory, a sequence of edges with consecutive vertices occurring on the path is considered as the definition of a path. The distance from node A to node B is therefore called the length of the path from A to B, if it exists, otherwise the distance is referred to as infinite.¹² The definition of distance based on path length fulfils all the conditions of being a metric (which were mentioned in the previous section of the chapter), so it is fully justified to transfer the concepts based on metrics, including the notion of a sphere with a given centre and radius, to the graph metric space. A sphere of radius r and centre K will be a set of nodes distant from K by no more than r, so no more than r-1 intermediate nodes will stand on the path from the centre of the sphere to the point A belonging to it.

We can use this concept of a sphere as a base for the notion of centre and periphery. If we assume that the centre is the sphere, then all sites that can be reached from the address at the centre of the sphere in no more than r steps will belong to it. The other addresses are peripheral to this site.

But is this exactly what we meant? Does such a designated centre in any way constitute the centre of the Internet? Probably not. The definition of a sphere represents a local centre, linked to a specific starting point, but it is nowhere near the understanding of the centre as the most important place, a vehicle for change, activity or a point of reference in global terms. It is impossible to carve out a centre by putting an above-average number of links on a site. Or rather, it was possible, but only in the initial phase of mass Internet access. The PageRank indicator mentioned above was intended to verify the centres thus generated by analysing the number and quality of links leading not from the site, but to it. And this, however, proved insufficient. Perhaps in economic terms, as an indicator of the profitability of advertising campaigns, the designation of the sites with the highest global metrics played its part, but in social terms it proved to fall short of growing demands, with current search algorithms relying much more on personalisation of the search results. The struggle to be ‘at the centre’ therefore takes on a whole new dimension.

THE GAME OF LIFE

Let us abandon the issue of dimension and distance for a moment and focus solely on the notion of neighbourhood and its impact on the development of the individual, while interpreting the individual itself, for example, as the nucleus, the centre of the work and creativity of a single artist, designer or author publishing and developing their activity in social media.

The cycle of existence of a website or a profile on a social network is based on a constant balance between life and death. This thread will invoke the aspect of overcrowding and loneliness as indicators heralding the twilight phase or the beginning of the development of the address under study. The discussion in the previous chapter, related to the question of centre and periphery on the Internet, made it possible to define the notion of neighbourhood as the set of all profiles that are one step away from a given centre, i.e., connected directly to the profile under study by the act of observation, making friends or joining a group. Can it be assumed, then, that in order to enhance the value of one’s place on the Internet, one must strive at all costs to broaden one’s neighbourhood by accumulating as many contacts as possible?

To answer this question, we will use the example of one of the first population growth simulators based solely on the neighbourhood definition and a few simple rules. The Game of Life is one of the more famous examples of a cellular automaton, popular not only because of its scientific potential, but because of its contribution to the field of culture and art. Invented in 1970 by British mathematician John Conway and popularised by Martin Gardner in the Scientific American journal,¹³ it served both research purposes – providing the opportunity to observe processes of development, decay or stabilisation of structures – and entertainment in the form of games and logic puzzles.

The game is played on a board (finite or infinite), divided into square cells. Each cell has eight neighbours – the cells that make up the neighbourhood adjoin it with their sides or corners, forming what is known as the Moore neighbourhood. Each cell can be in one of two states: it is either ‘alive’ (active) or ‘dead’ (inactive). The survival of a given cell in the current cycle is defined as follows:

•  a dead cell that has exactly three living neighbours becomes alive in the next time unit;

•  a living cell that has two or three living neighbours is still alive;

•  with any other number of neighbours, the living cell dies: either from ‘loneliness’ with fewer than two living neighbours or from ‘overcrowding’ when there are four or more neighbours.

Figure 4. An example of the state of a cellular automaton in Conway’s Game of Life

How do the rules of Conway’s game relate to the cycle of life on the Internet? Whether a profile or website is set up spontaneously or preceded by a series of market analyses and preparations, the key issue is to gather a specific community around the place being created. We will now focus on a very specific thread that is an attempt to describe the evolution of the size and character of this community. Let us assume, as it was in Conway’s case, that one cell is one individual: an on-line profile in our case. Let us further assume that its neighbourhood includes any other profile with which it is in active contact, which in this case could mean commenting on each other’s content, engaging in dialogue or tagging each other in posts. Here, of course, we have to deviate from the plane geometry considered in the original Game of Life because the plane described with Moore’s eight-neighbourhood scheme makes it impossible to assign to cells the number of contacts that applies to web profiles; from the mathematical perspective, however, this is not a problem. We can assign two states to a cell. Conway’s dead (inactive) cell would have an analogy in the form of a user profile that is dormant, passive, with limited on-line activity, or focused solely on receiving messages rather than on transmitting them. The equivalent of a live cell, on the other hand, would be a profile that has a large number of active contacts with which it regularly exchanges content and is geared towards growth and expansion, which may also include advertising contracts and influencer activities.

On the face of it, it would seem that gaining more contacts every time is absolutely desirable and guarantees the success of the profile. However, applying the principles of cellular automaton to the above description¹⁴ leads to quite the opposite conclusion. In any case, there is a certain critical value of the number of contacts beyond which the addition of another new one entails the loss of existing ones; moreover, the process can proceed exponentially, leading to the loss of value (or to death?) of the entire profile. The phenomenon of losing contacts by exceeding a limit number of contacts has been investigated on Instagram¹⁵ and Twitter¹⁶ and is closely related to the user behaviour captured in the follow/unfollow pattern, which consists of extensively sending out invitations to follow one’s own profile while at the same time adding the profiles of invitees to our own followed ones. If there is no interest from the invited guests, the profile manager also removes their follows from the profile in question. This process, especially when carried out on a large scale and aided by the operation of bots, does not ultimately add value, as it is an artificial activity, the contact with the people invited is often one-off and – in the absence of further interaction – eventually cut off by one of the users. Moreover, as it creates chaos in the popularity rankings of profiles, it is banned by many portals, as indicated in the terms & conditions of use.¹⁷

THE CURSE OF MULTIDIMENSIONALITY

Returning to the issues of dimension and distance raised in earlier chapters, let us now look at the ‘density’ of social media contacts. Let us pose the question: will adding a new contact to a friend group broaden the possibility of effective communication among relevant users or, paradoxically, might it have a narrowing effect?

From the geometric perspective, if we deploy a certain number of points in a spatial unit, e.g., five points per one centimetre square, and then allow the points in question to ‘bounce around’ in a space one dimension larger – in this case a cube with a side of one centimetre – the density of point distribution drops dramatically. This can be imagined by dividing the original space, a square with a side of one centimetre, into smaller squares with a side of one millimetre, which gives us 10 × 10 = 100 such squares. If we arrange the points so that there is at most one point in one square, the probability of drawing a square containing a point is five in a hundred, or 5%. If we extend the reasoning from square to cube, the division results in 10 × 10 × 10 = 1,000 smaller cubes, and if we keep the rule of only allowing one point in one cube, the chance of drawing a cube with a point is five in a thousand, or barely 0.5%. Furthermore, as the dimension increases, a sphere with the given radius occupies an increasingly smaller portion of a cube with a fixed edge length, so the probability that, for a given point, another of the highlighted points will be found in the surrounding neighbourhood also decreases. Hence ‘In high dimensional spaces, no one can hear your scream’ in the introduction to the article; – if your voice only spreads over a given distance, it is likely that in hyperspace there will be no one close enough to hear it ….

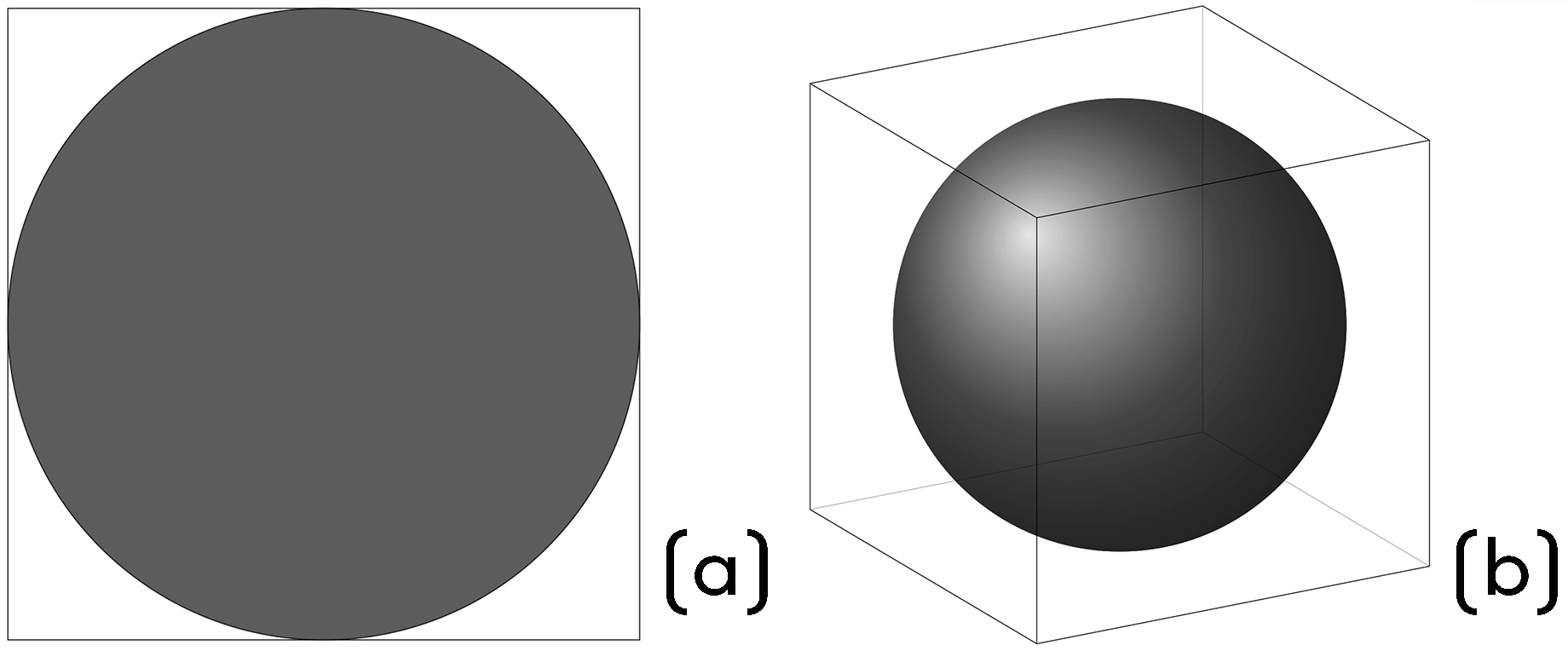
Figure 5. A sphere in two dimensions fills more of the square into which it is inscribed than a sphere in three dimensions fills a cube.

How, then, does geometric dimensional expansion relate to making more contacts on social networks? Every profile activity, including adding a contact to a friend group, liking, following, and joining a group, causes the content distribution algorithm to learn our preferences and multiply the number of suggested posts, adding more and more of those not coming from our direct contacts.

Let us specifically use the example of Facebook and the question: How does Facebook distribute content? According to the official data,¹⁸ Facebook displays messages on a user’s homepage by performing analysis in four main steps, including selecting content shared by the user’s contacts, collecting signals and predictions of how likely a user is to respond to a post, and calculating the relevance index, i.e., how interested the audience will be in a post.

So, is it possible to predict who will see the content of the message we are about to edit and send out to the world, and when will this happen? We would like to believe that the message will at least be read by the owners of the profiles we have in our friends tab. But what if, for each of our friends, we are just one of several hundred or even several thousand contacts, each of whom sends at least a few messages a week? The likelihood of our post being high enough for our friends to see it on their home page decreases with every friend contact they add, just as the chance of finding a point within range of a sphere of a given radius decreases with every increase in the dimension in which it is located. Unless our profile has an advantage over others in terms of the relevance of the content published, the closeness of the relationship expressed by frequent interaction or the skilful construction of the message itself, no one may hear us. Despite the Friends tab filled to the brim.